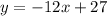Parallel lines have the same slopes and different y-intercepts
We will find the slope of the parallel line, then take it as a slope of line b
The rule of the slope is

Where (x1, y1) and (x2, y2) are two points lie on the line
Since the parallel line passes through the points (1, 5), (2, -7), then
x1 = 1 and x2 = 2
y1 = 5 and y2 = -7
Substitute them in the rule above
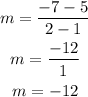
Since parallel lines have the same slope, then the slope of line b is -12
Since the slope-intercept form of the linear equation is

Then the equation of line b is
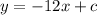
To find c substitute x and y by the coordinates of any point lies on line b
Since line b is passed through the point (1, 15), then
x = 1 and y = 15
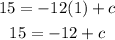
Add 12 to both sides to find c
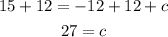
Then the equation of line b is