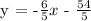From the given: Slope (m) = -6/5 and point (-9, 0), we will use the Slope-Intercept Form in making the equation.
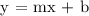
The slope-intercept form is given a y=mx+b where m is the slope and b is the y-intercept at point (0,b).
Let's solve for the y-intercept (b) substituting the slope (m) = -6/5 and (x,y) = (-9,0).
Thus, we get,
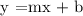
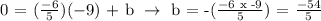
Let's now make the equation substituting the slope (m) = (-6/5) and y-intercept (b) = (-54/5). We get,