Question

A line has a slope of -4/5 wich ordered pairs could be points on a line that is a perpendicular to this line?two options (-2,0) and (2,5) (-4,5) and 4,-5) (-3,4) and (2,0)(1,-1) and (6,-5)(2,-1) and (10,9)Please hurry

Answer 1

Step 1

Given;

`\begin{gathered} A\text{ line with a slope of }(-4)/(5) \\ m_1=(-4)/(5) \end{gathered}`

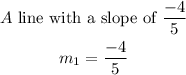
Required;

`To\text{ find the ordered pairs that could be points on a perpendicular line.}`

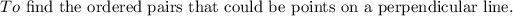
Step 2

Write the relationship between the slopes of perpendicular lines and find the slope of the perpendicular line

`\begin{gathered} m_2=-\frac{1_{}}{m_1} \\ m_2\text{ is the slope of the perpendicular line} \\ m_2=-(1)/((-4)/(5)) \\ m_2=-1*(-(5)/(4)) \\ m_2=(5)/(4) \end{gathered}`

Step 3

Given the points, and applying the formula of the slope can check the points thus

`\begin{gathered} 1)\text{ }(5-0)/(2-(-2))=(5)/(4) \\ 2)(-5-5)/(4-(-4))=(-10)/(8)=-(5)/(4) \\ \end{gathered}`
`\begin{gathered} 3)\text{ }(0-4)/(2-(-3))=-(4)/(5) \\ 4)(-5-(-1))/(6-1)=(-4)/(5) \\ 5)(9-(-1))/(10-2)=(10)/(8)=(5)/(4) \end{gathered}`

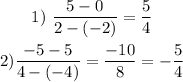
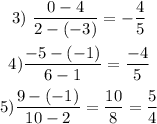
Hence the answer is option 1

written as ( -2,0) and (2,5)

and

Option 5

written as (2,-1) and (10,9)

`