Question

The cue ball approaches a stationary ball of equal mass at 4.00 m/s. After the collisionthe balls separate, the velocity of each ball making a 45.0° angle with the cue ball’soriginal path just on opposite sides. If the effects of spin and rolling are negligible,determine the velocity of both balls after the collision.

Answer 1

Given data:

* The initial velocity of the cue ball is 4 m/s.

* The angle made by the final velocity with the initial direction of motion is 45 degrees.

Solution:

The initial momentum of the system along the initial direction of motion of cue ball is,

`p_1=mu_1+mu_2`

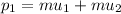
where m is the mass, u_1 is the initial velocity of the cue ball and u_2 is the initial velocity of the other ball,

As the other ball is stationary, thus the value of u_2 is zero.

The initial momentum of the system is,

`\begin{gathered} p_1=m*4+0 \\ p_1=4m \end{gathered}`

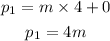
The final momentum of the system is,

`p_2=mv_1cos(45^(\circ))+mv_2cos(45^(\circ))`

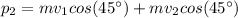
The diagrammatic representation of the given system is,

By the law of conservation of momentum, the initial momentum of the system is equal to the final momentum of the system,

Thus,

`\begin{gathered} p_1=p_2 \\ 4m=mv_1\cos (45^(\circ))+mv_2\cos (45^(\circ)) \end{gathered}`

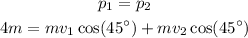
As the magnitude of the velocity is the same after the collision, thus,

`\begin{gathered} 4m=mv\cos (45^(\circ))+mv_{}\cos (45^(\circ)) \\ 4=v_{}\cos (45^(\circ))+v_{}\cos (45^(\circ)) \\ 4=2v\cos (45^(\circ)) \\ v=(4)/(2\cos (45^(\circ))) \\ v=2.83\text{ m/s} \end{gathered}`

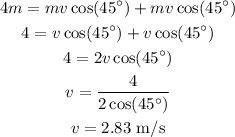
Thus, the velocity of each ball after the collision is 2.83 meters per second.