Assuming that the lines FG and HG are tangent, you need to remember that, by definition, when two tangents intersect outside a circle, the angle formed by them is the difference of the intercepted arcs divided by 2.
Then:

In this case, you know that the angle formed by the tangents FG and HG is:

And the Intercepted arcs are the following:
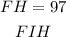
By definition, a circle has 360 degrees; then you can find the measure of the arc FIH as following:
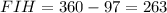
Knowing that, you can substitute values into the equation in order to find the measure of the angle FGH:

The answer is: First option.