Question

A company has made a rubber ball for $0. 02 per square foot. The company wants to spend a maximum of $1 each on a new ball.What is the diameter of the new ball to the nearest tenth of a foot?A.4. 6 feetB.2. 9 feetC.5. 8 feetD.2. 3 feet

Answer 1

Solution:

How to find the diameter of the ball?

Remember that for a sphere of diameter D, the surface area is:

`\begin{gathered} A=4\pi((D)/(2))^2 \\ r=(D)/(2) \end{gathered}`

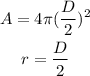
In this case, the cost is $0.02 per square foot, and the company wants to expend (at maximum) $1 per ball, so first we need to solve:

`\begin{gathered} 0.02* A=1 \\ A=(1)/(0.02) \\ A=50 \end{gathered}`

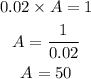
By substituting the values of A=50 in the formula below, we will have

`\begin{gathered} \begin{equation*} A=4\pi((D)/(2))^2 \end{equation*} \\ 50=4*(22)/(7)*((D^2)/(4)) \\ 50=(22D^2)/(7) \\ cross\text{ multiply} \\ 50*7=22D^2 \\ 22D^2=350 \\ (22D^2)/(22)=(350)/(22) \\ D^2=(350)/(22) \\ D=\sqrt{(350)/(22)} \\ D=4.0feet \end{gathered}`

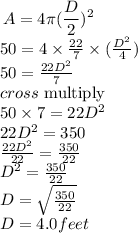
Hence,

Since the company wants to spend a maximum $1,

The diameter of the new rubber ball, to the nearest foot, must be D = 4.0 ft (in the case of the maximum cost).

Hence,