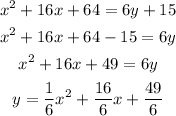Since the directrix is y=-4, use the equation of a parabola that opens up or down.
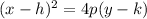
where vertex is at (h,k) and focus is at (h,k+p)
The vertex is halfway between the directrix and focus. Find the y-coordinate of the vertex using the following
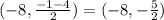
Find the distance from the focus to the vertex.
The distance from the focus to the vertex and from the vertex to the directrix is |p|. Subtract the y-coordinate of the vertex from the y-coordinate of the focus to find p.
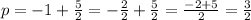
Substitute in the known values for the variables into the equation
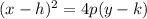
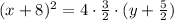
Simplify
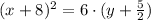
in y=ax^2+bx+c form: