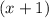Recall that a rational function:
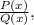
has a vertical asymptote at x₀ if and only if:
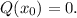
Also, the roots of the above rational function are the same as P(x).
Since the rational function has a vertical asymptote at x=-1, we get that its denominator must be:
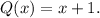
Since the rational function has a double zero at x=2 we get that its numerator must be of the form:
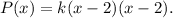
Finally, since the rational function has y-intercept at (0,2) we get that:

Simplifying the above equation we get:
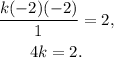
Dividing the above equation by 4 we get:
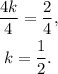
Therefore, the rational function that satisfies the given conditions is:
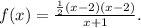
Answer:
The numerator is:
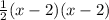
The denominator is: