Question

Find a possible function f(n) whose domain is a set of natural numbers and whose outputs are the terms of the sequence. -4^1, 4^(-1/2), 1, 4^(1/2), 4

Answer 1

we have the sequence

4^=-1, 4^(-1/2), 1, 4^(1/2), 4​

so

a1=4^-1=1/14

a2=4^(-1/2)=(1/4)^(1/2)=1/2

a3=1

a4=4^(1/2)=2

a5=4

therefore

a2/a1=(1/2)/(1/4)=2

a3/a2=1/(1/2)=2

a4/a3=2/1=2

a5/a4=4/2=2

that means

Is a geometric sequence and the common ratio is r=2

the general formula is equal to

`f(n)=a1\cdot(r)^((n-1))`

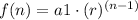
substitute given values

a1=1/4

r=2

`f(n)=(1)/(4)\cdot(2)^((n-1))`

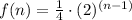
we have the function f(n)

Verify the outputs

For n=1

substitute

`\begin{gathered} f(1)=(1)/(4)\cdot(2)^((1-1)) \\ f(1)=(1)/(4)\cdot(2)^((0)) \\ f(1)=(1)/(4)=4^(-1) \end{gathered}`

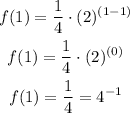
For n=2

`\begin{gathered} f(2)=(1)/(4)\cdot(2)^((2-1)) \\ f(2)=(1)/(4)\cdot(2)^((1)) \\ f(2)=(1)/(2) \end{gathered}`

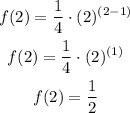
the general expression is

`f(n)=(1)/(4)\cdot(2)^((n-1))`

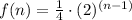
Remmeber that

(1/4)=4^-1=(2^2)^-1=2^-2

substitute in the given expression

`\begin{gathered} f(n)=(1)/(4)\cdot(2)^((n-1)) \\ f(n)=(2)^((-2))\cdot(2)^((n-1)) \end{gathered}`

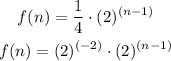
Adds the exponents

-2+(n-1)=n-3

therefore

`f(n)=2^((n-3))`

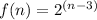
an equivalent expression