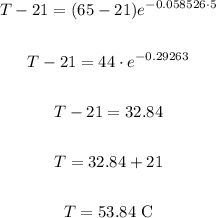Question

Water at 100 oC is taken off the stove and allowed to cool for 10 minutes. In this 10minutes, the temperature decreased to 65 oC. Given that the room temperature is 21oC, find the temperature of the water in degrees Celsius after an additional 5 minutes waiting time and on condition that the Newton’s Law of cooling is not violated

Answer 1

In order to calculate the temperature after 5 more minutes, we can use the Newton's Law of cooling:

`T-T_s=(T_0-T_s)e^(kt)`

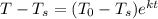
Where Ts is the ambient temperature and T0 is the initial temperature.

So, using Ts = 21, T0 = 100, T = 65 and t = 10, let's calculate the value of k:

`\begin{gathered} 65-21=(100-21)e^(10k)\\ \\ 44=79e^(10k)\\ \\ e^(10k)=(44)/(79)\\ \\ \ln(e^(10k))=\ln((44)/(79))\\ \\ 10k=-0.58526\\ \\ k=-0.058526 \end{gathered}`

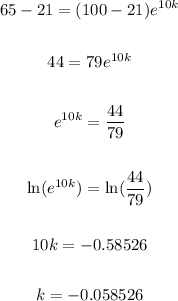
Now, let's use T0 = 65 and t = 5 to calculate the value of T:

`\begin{gathered} T-21=(65-21)e^(-0.058526\cdot5)\\ \\ T-21=44\cdot e^(-0.29263)\\ \\ T-21=32.84\\ \\ T=32.84+21\\ \\ T=53.84\text{ \degree C} \end{gathered}`