Question

1) A ball is thrown downward from a window in a tall building. Its position at time t in seconds iss(t) = -16t2 + 32t + 55, where s(t) is in feet. How long (to the nearest tenth) will it take the ball to hit the ground?A)-1.2 secB) 1.2 secC) 2.9 secD) 3 sec

Answer 1

The equation for the position is,

`s(t)=-16t^2+32t+55`

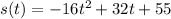
When the ball hit the ground then value of height is 0 feet. So value of s(t)=0,

The equation for the time is,

`-16t^2+32t+55=0`

Determine the roots of the equation by using the quadratic formula.

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ =\frac{-32\pm\sqrt[]{(32)^2-4(-16)(55)}}{2(-16)} \\ =\frac{-32\pm\sqrt[]{4544}}{-32} \\ =(-32\pm67.41)/(-32) \\ =(-99.41)/(-32),\text{ }(35.41)/(-32) \\ =3.10,-1.10 \end{gathered}`

The value of time can never be less than 0. so approximate value of time is 3 seconds. Correct option is D part.