I just need some help solving this question, i’m not sure what to do

Question

asked Jan 12, 2023 178k views

1 Answer

Bret Copeland · Answer 1 · 2023-01-16T10:49:42+0000

From the double-angle identity,

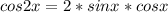
we can rewritte our given equation as:

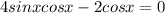
By factoring 2cosx on the left hand side, we have

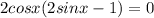
This equation has 2 solutions when

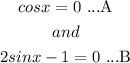
$\begin{gathered} cosx=0\text{ ...\lparen A\rparen} \\ and \\ 2sinx-1=0\text{ ...\lparen B\rparen} \end{gathered}$

From equation (A), we obtain

$x=(\pi)/(2)\text{ or }(3\pi)/(2)$

and from equation (B), we have

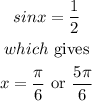
$\begin{gathered} sinx=(1)/(2) \\ which\text{ gives} \\ x=(\pi)/(6)\text{ or }(5\pi)/(6) \end{gathered}$

On the other hand, we can find one more solution from the original equation by substituting x=0, that is,

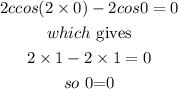
$\begin{gathered} 2ccos(2*0)-2cos0=0 \\ which\text{ gives} \\ 2*1-2*1=0 \\ so\text{ 0=0} \end{gathered}$

then, x=0 is another solution. In summary, we have obtained the following solutions:

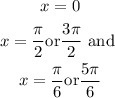
$\begin{gathered} x=0 \\ x=(\pi)/(2)\text{or}(3\pi)/(2)\text{ and } \\ x=(\pi)/(6)\text{or}(5\pi)/(6) \end{gathered}$

However, the intersection of the last set is empty. So the unique solution is x=0 as we can corroborate on the following picture:

Therefore, the solution set is: {0}