We can notice the triangle on the square, hypotenuse is 8m and the base is half of the lengt of the square we will name it x
then
we can use pythagoras to solve
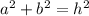
where a and b aer sides of the triangle and h the hypotenuse
replacing
![\begin{gathered} x^2+x^2=8^2 \\ 2x^2=64 \\ x^2=(64)/(2) \\ \\ x=\sqrt[]{32}=4\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ge9trsiaj6xmqjklrmsfo924sm1t3y16jf.png)
the length of x is half of the side of the square then the side of the square is
![4\sqrt[]{2}*2=8\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/lv3d1omwiyxhc0rjiyjbetd9eoriwe3z2n.png)
each side of the square is 8v2 meters
Area
we use formula of the area
![\begin{gathered} A=l* l \\ A=8\sqrt[]{2}*8\sqrt[]{2} \\ \\ A=128 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/begfcao79c347c8qqel03agrwagjfumiop.png)
area of the square is 128 square meters
Perimeter
we use formula of the perimeter
![\begin{gathered} P=4l \\ P=4*8\sqrt[]{2} \\ P=32\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bowaqllvrd1n9gyj80dbhep1oamygwr2sg.png)
perimeter of the square is 32v2 meters