Solution
Given a triangle XYZ on the graph
The coordinates of points X, Y and Z are
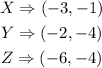
To find the approximate length of the sides, we apply the formula to find the distance, d, between two points which is
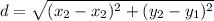
To find the approximate length of side XY, substitute the coordinates of points X and Y into the formula to find the distance, d, between two points
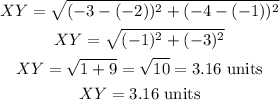
Hence, the approximate length of side XY is 3.16 units (option b)