Since x represents the total amount of dollars in Ariella's sales, and she earns a commission of 15% over her sales, then multiply x by 15/100 to find the commision that Ariella earns:
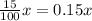
She earns a salary of $275 additional to the comission for her sales. Then, the model that represents the amount of money that Ariella makes after x dollars in sales is:

Step 1:
The y-intercept is the value of y when x=0. It can be identified in the equation as the constant term, in this case, 275. The ordered pair (0,275) represents the point in the coordinate plane where the graph of y=0.15x+275 intercepts the Y-axis.
Therefore, the y-intercept is (0,275) and the y-coordinate represents Ariella's base weekly salary.
Step 2:
The slope is the coefficient of the variable x. In general, it represents the rate of change of the variable y with respect to x, i.e. the amount by which the variable y increases when x increases 1 unit. In the context of the problem, we can see that it represents the commission rate.
Therefore, the slope is 0.15 and it represents the commission rate that Ariella gets for her sales.
Step 3:
The equation of a line with slope m and y-intercept b in slope-intercept form is:

As explained above, the slope for this model is 0.15 and the y-intercept is 275.
The equation shown in the beginning of the explanation was already written in slope-intercept form.
Therefore, the quation in slope-intercept form that models this situation is:
