To find the lateral area of a right triangular prism, apply the formula:
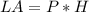
Where:
P is the perimeter of the base
H is the height
To find the perimeter of the traingular base, apply the perimeter of a triangle formula:
P = a + b + c
Let's find the third side of the traingular base using the pythagorean theorem.
We have:
![\begin{gathered} c^2=a^2+b^2 \\ \\ c^2=4^2+3^2 \\ \\ c^2=16+9 \\ \\ c^2=25 \\ \\ \text{Take the square root of both sides:} \\ \sqrt[]{c^2}=\sqrt[]{25} \\ \\ c=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/crw3esjp9auxjsbavi2vzp8z8q1h3ep8gu.png)
Thus, the perimeter of the base is:
P = 3 + 4 + 5 = 12
Hence, to find the lateral area, we have:
LA = P x H
Where:
Perimeter of base, P = 12
Height, H = 8
LA = 12 x 8 = 96
Therefore, the lateral area of the right traingular prism is 96 square units.
ANSWER:
96