Question

Select the point that is on the line through (10,4) and (3,9)

Answer 1

,Step 1:

First determine the slope-intercept form of the equation of a line.

`\text{Slope = }(y_2-y_1)/(x_2-x_1)\text{ = }(y-y_1)/(x-x_1)`

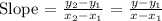
Step 2:

Next, substitute all values to find the equation of a line.

`\begin{gathered} x_1\text{ = }10 \\ y_1\text{ = 4} \\ x_2\text{ = 3} \\ y_2\text{ = 9} \\ \frac{y\text{ - }4}{x\text{ -10}}\text{ = }\frac{9\text{ - 4}}{13\text{ - 10}} \\ \frac{y\text{ - 4}}{x\text{ - 10}}\text{ = }(5)/(3) \\ 3y\text{ - 12 = 5x - 50} \\ 3y\text{ - 5x = }-38 \end{gathered}`

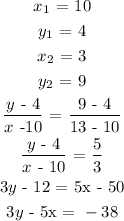
Substitute x and y from each option, any option that results in -38 is the answer.

Final answer

Option C

Let check

3y - 5x = -38

3(14) - 5(16)

42 - 80 = -38