We have to calculate the number of children (C) and the number of adults (A) that were admitted.
The number of people, that is the sum of the children and the adults, is 282. Then, we can write:
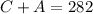
The ticket collection was $748, where each children pay $1.5 and each adult pays $4. Then, we can write:

Now, we have a system of 2 equations with 2 unknowns. We can solve it by substitution, using:
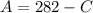
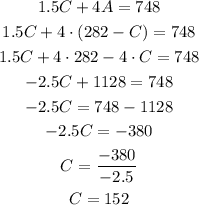
Now that we know the number of children C, we can calculate the number of adults A as:

Answer:
Number of children = 152
Numbre of adults = 130