Solution:
Given the circle with diameter AB as shown below
The circumference of the circle is expressed as

Thus, equation 1 becomes
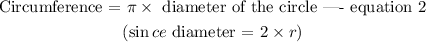
Given that the diameter AB of the circle is 28 ft, the circumference of the circle will be evaluated as
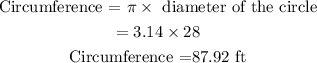
Hence, the circumference of the circle is 87.92 ft.