Question

The perimeter of a rectangle is 140 feet. The length is 10 more than 4 times the width. Find the length and width.

Answer 1

Let the length and width be represented by l and w respectively.

The perimeter is calculated using the formula:

`P=2(l+w)`

Given that the perimeter is 140 feet, the equation above can be written as:

`2(l+w)=140`

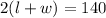
The length is given to be 10 more than 4 times the width. This statement is written as a mathematical statement as:

`l=10+4w`

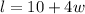
This equation gives the measure of the length.

Substitute the equation for l into the perimeter equation:

`\begin{gathered} 2(10+4w+w)=140 \\ \text{ Divide both sides by 2:} \\ 10+5w=70 \\ \text{ Subtract 10 from both sides of the equation:} \\ 5w=60 \\ \text{ Divide both sides by 5:} \\ w=12 \end{gathered}`

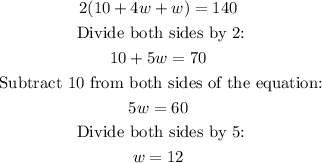
Substitute the value for w into the equation giving the measure of l:

`\begin{gathered} l=10+4(12) \\ l=10+48 \\ l=58 \end{gathered}`

Therefore, the length is 58 feet and the width is 12 feet.