Answer:
52
Explanation:
Here it's given that p is inversely proportional to the square of q. We can write this mathematically as ,
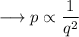
Let k be the constant of proportionalality .
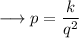
Again it's given that when p is 13 , q is 4 . On substituting this in the above equation we can find out the value of k , as ;
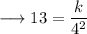
Solve out for k ,
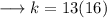
Multiply ,
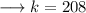
Again when the value of q is 2 , we need to find out the value of p . So ,
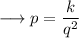
Substitute ,
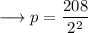
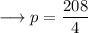
Simplify,
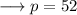
This is the required answer.