Question

What is the GCF of 525, 135, 750

Answer 1

GCF is the greatest common factor of some numbers

We need to find the GCF of 525, 135, 750

Since all the numbers end by 5 or 0, then

All of them can divide by 5

Then the first common factor of them is 5

`\begin{gathered} (525)/(5)=105 \\ (135)/(5)=27 \\ (750)/(5)=150 \end{gathered}`

Since the sum of digits of 105 = 1 + 0 + 5 = 6, and 6 can divide by 3

Then 3 is a factor of 105

Since The sum of the digits of 27 = 2 + 7 = 9 and 9 can divide by 3

Then 3 is a factor of 27

Since the sum of the digits of 150 = 1 + 5 + 0 = 6 and 6 can divide by 3

Then 3 is a factor of 150

Then 3 is the second common factor of them

`\begin{gathered} (105)/(3)=35 \\ (27)/(3)=9 \\ (150)/(3)=50 \end{gathered}`

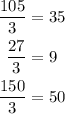
Since 35, 9, and 50 can not divide by the same number, then

The greatest common factor of 525, 135, 750 is

`\begin{gathered} \text{GCF}=5*3 \\ \text{GCF}=15 \end{gathered}`

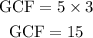
The GCF of 525, 135, and 750 is 15