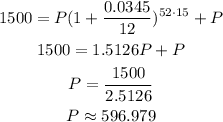Question

11. Andrew is planning for retirement, and he estimates that he'll want to be able to withdraw $1,500 each week for 15 years once he retires. He opens a Roth IRA and finds investments that he expects to return 3.45% interest compounded weekly.(a) How much will he need to have in the account when he retires in order to meet his goal? $(b) How much will he have to deposit each week for the next 40 years in order to get this balance at retirement? $(c) How much interest will his deposits earn between now and retirement? $

Answer 1

Consider that the principal (P) invested at an annual rate of interest (R) for time (T) compounded as per the number of periods (n), gives an amount (A) of,

`A=P(1+(R)/(n))^(nT)`

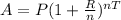
The corresponding interest is given by,

`\begin{gathered} CI=A-P \\ CI=P(1+(R)/(n))^(nT)-P \end{gathered}`

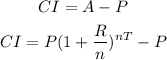
According to the given problem,

`\begin{gathered} CI=1500 \\ T=15 \\ R=3.45\text{ percent}=0.0345 \\ n=52 \end{gathered}`

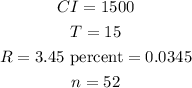
Substitute the values,

`\begin{gathered} 1500=P(1+(0.0345)/(12))^(52\cdot15)+P \\ 1500=1.5126P+P \\ P=(1500)/(2.5126) \\ P\approx596.979 \end{gathered}`