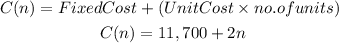a. Based on the table, when 200 units is produced, the cost of production is $12,100 hence, C(200) = $12,100.
On the other hand, when 150 units is produced, the cost of production is $12,000 hence, C(150) = $12,000.
Subtracting C(200) - C(150), we have $100.
Dividing this result $100 by the difference of 200 and 150, we get 2.
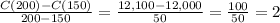
b. Estimate C(0).
Based on the answers in letter a, we can see that for every additional unit produced, the additional cost of production is $2.
So, if we subtract 100 units, there will be 2*100 = $200 less on the cost of production.
From $11, 900 total cost of production of 100 units as shown in the table, we remove 100 units that cost $200, the total cost of production will now be $11, 700. Hence, at 0 units produced, the cost of production is $11, 700. C(0) = $11, 700.
c. Based on the answer in letter b, with 0 units produced, there is already a fixed cost of $11, 700.
Based on the answer in letter a, the unit cost per number of units produced is $2. If "n" is the number of units produced, the additional cost is 2n.
With these information, the formula for the finding the total cost of production is: