Question

Kurt can ride his bike for 30 miles with the wind in the same amount of time that he go 21 miles against the wind. If the winds speed is 6 mph, what is Kurt’s speed on his bike

Answer 1

In this question, we are given the following:

Kurt can ride his bike for 30 miles with the wind in the same amount of time that he goes 21 miles against the wind. If the wind's speed is 6 mph, what is Kurt’s speed on his bike?

Step 2:

The details of the solution are as follows:

Let Kurt's speed on the bike be U,

Kurt can ride his bike for 30 miles with the wind in the same amount of time,

If the wind's speed is 6 mph, it means that:

`(\text{ U+ 6 \rparen t = 30 -- equation 1}`

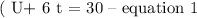
If he goes 21 miles against the wind and the wind's speed is 6 mph, it means that:

`(U-6)t\text{ = 21 --- equation 2}`
`\begin{gathered} solving: \\ (U+6)t\text{ = 30 --equation 1} \\ (U-6)t\text{ = 21 --equation 2} \\ Divide\text{ equation 1 by equation 2, we have that:} \\ \end{gathered}`
`\begin{gathered} \frac{(U+6)t\text{ }}{(U-6)t\text{ }}=\text{ }(30)/(21) \\ Then,\text{ we have that:} \\ 21\text{ \lparen U+6 \rparen = 30 \lparen U-6 \rparen} \\ 21U\text{ + 126 = 30 U -180} \\ collecting\text{ like terms, we have that:} \\ 126+\text{ 180 = 30 U -21 U} \\ 9U\text{ = 306} \\ Divide\text{ both sides by 9, we have that:} \\ U\text{ = }(306)/(9) \\ U\text{ = 34 miles per hour} \end{gathered}`

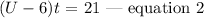
CONCLUSION:

Kurt's speed on his bike = 34 miles per hour