Let x be the cost of one corsage, and y be the cost of one boutonniere, then we can set the following system of equations:
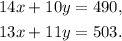
Solving the second equation for y, we get:
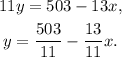
Substituting the above equation in the first one we get:
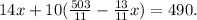
Solving for x, we get:
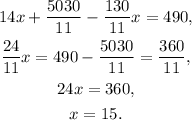
Substituting x=15 in the equation that we solved for y we get:
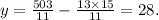
Answer: A corsage sells for $15, and a boutonniere sells for $28.