Question

I need help with this math problem question number 2 please

Answer 1

The first question is true because a one-to-one function always has a different value in y.

For the second you need to find the inverse function to conclude that the function that they give you is correct. So

The first step is to replace the x with y and the y with x:

`y=4x+3`
`x=4y+3`
`4y=x-3`
`y=(x-3)/(4)`

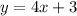
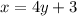
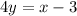
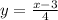
We find the same function as g(x). So the question is true.

For question 3, to discard a slant asymptote subtract the grade of the denominator from the numerator, if it is one we have a slant asymptote, else we don't have a slant asymptote:

`2-2=0`

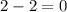
We don't have slant asymptote, now find the vertical asymptotes

Equal the denominator to 0 and solve:

`9x^2-6=0`
`9x^2=6`
`x^2=(6)/(9)`
`x^2=(2)/(3)`
`x=\sqrt{(2)/(3)},-\sqrt{(2)/(3)}`

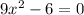
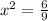
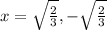
We have vertical asymptotes in these 2 values of x

Finally for horizontal asymptotes:

Find the limit of the function when x tends to infinity:

`\lim _(x\to \infty )\left((-5x+2x^2)/(9x^2-6)\right)`

Divide for the denominator with the greatest potency:

`\lim _(x\to \infty \:)\left((-(5)/(x)+2)/(9-(6)/(x^2))\right)`

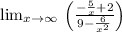
Separate terms

`(\lim _(x\to \infty \:)\left(-(5)/(x)+2\right))/(\lim _(x\to \infty \:)\left(9-(6)/(x^2)\right))`

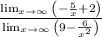
Solve each one:

`\lim_(x\to\infty\:)\left(-(5)/(x)+2\right)=-\lim_(x\to\infty\:)\left((5)/(x)\right)+\lim_(x\to\infty\:)\left(2\right)=0+2=2`
`\lim_(x\to\infty\:)\left(9-(6)/(x^2)\right)=\lim_(x\to\infty\:)\left(9\right)-\lim_(x\to\infty\:)\left((6)/(x^2)\right)=9-0=9`

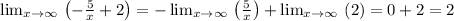
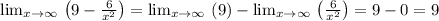
Replace:

So have a horizontal asymptote in 2/9