We have a sample of 600 values.
They belong to a population that have a mean of 18.5 and a standard deviation of 3.25.
We have to calculate the expected proportion of those values that will lie between 21 and 27.
We can do it calculating the z-scores for each extreme of the interval [21, 27]:
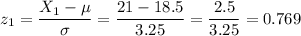
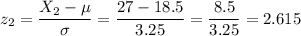
Then, we can approximate the proportion as the probability of this interval:
![\begin{gathered} P(21As the proportion is 0.197, the number of values will be:[tex]Y=p\cdot N=0.197\cdot600=118.2\approx118]()
From the options, 130 is the closest number to our estimation.
Answer: 130