Question

Two equally charged, 4.454 g spheres are placed with 2.105 cm between their centers. When released, each begins to accelerate at 349.026 m/s2. What is the magnitude of the charge, in micro-Coulombs, on each sphere?

Answer 1

First, let's calculate the electric force needed to generate this acceleration, using the second law of Newton:

`\begin{gathered} F=m\cdot a\\ \\ F=0.004454\cdot349.026\\ \\ F=1.554562\text{ N} \end{gathered}`

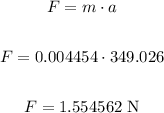
Now, let's use the formula for the electric force, so we can calculate the charge q of each sphere:

`\begin{gathered} F_e=(K\cdot q_1\cdot q_2)/(d^2)\\ \\ 1.554562=(9\cdot10^9\cdot q^2)/(0.02105^2)\\ \\ q^2=(1.554562\cdot0.02105^2)/(9\cdot10^9)\\ \\ q^2=7.65367\cdot10^(-14)\\ \\ q=2.7665\cdot10^(-7)\\ \\ q=0.277\cdot10^(-6)\text{ C}=0.277\text{ }\mu C \end{gathered}`

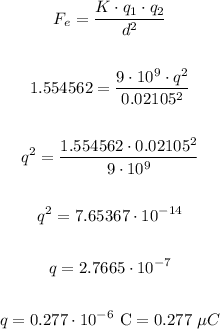
Therefore the charge of each sphere is 0.277 micro-Coulombs.