Exponential function
Part A
We know that
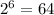
then
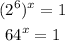
then, we want to find a value of x so if we multiply x times 64 it will be 1.
We know that any number with exponent 0 is 1:
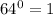
Then x = 0
Part B
Since any number with exponent 0 is 1, then:
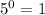
Then,
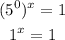
So, we want to find a number for x so if 1 is multiplied x times it will be 1.
Everytime 1 is multiplied by itself the answer is 1:
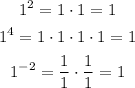
Then, x is any number
x = ..., -2, -1, 0 , 1, 2, ...