Part A
The functions would be:
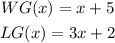
Part B
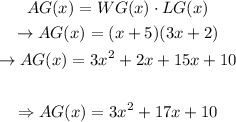
Part C
Let's evaluate x = 7 in AG(x)
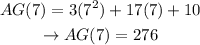
Thereby, the area of the garden would be 276 square feet
Part D
The functions would be:
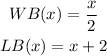
Part E
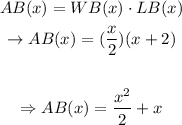
Part F
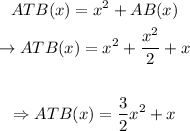
Part G
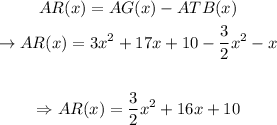
Part H
We have a function for the area of the bell pepper patch in terms of x, the measurement of the lenght and width of the tomato patch. This is:
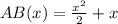
We know the value of this area. This way, we can solve the equation for x,
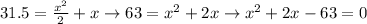
Using the cuadratic formula, and ignoring non-positive results, we'll get that
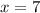
Now, plugging in this value in AR(x),
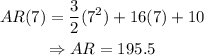
This way, we can conclude that the remaining space in the garden after planting tomatoes and bell peppers is 195.5 square feet