Question

How to solve inequality 3x - y > 2 2x + y > 3

Answer 1

The graph of an inequality is a region in the Cartesian plane. To know which line is the limit of the graphical region, the inequalities are as if they were equations, that is, graph the following lines:

`\begin{gathered} 3x-y=2\text{ (1)} \\ 2x+y=3\text{ (2)} \end{gathered}`

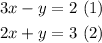
To do this, first clear y in each of the equations:

First equation

`\begin{gathered} 3x-y=2 \\ \text{ Subtract 3x from both sides of the equation} \\ 3x-y-3x=2-3x \\ -y=2-3x \\ \text{ Multiply by -1 on both sides of the equation} \\ (-y)\cdot-1=(2-3x)\cdot-1 \\ y=-2+3x \end{gathered}`

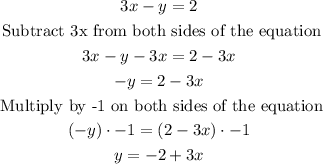
Second equation

`\begin{gathered} 2x+y=3 \\ \text{ Subtract 2x from both sides of the equation} \\ 2x+y-2x=3-2x \\ y=3-2x \end{gathered}`

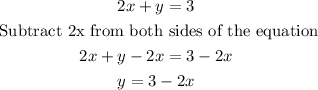
Now, give x values ​​that are within the domain of each equation and replace them in each equation to find its corresponding value in y:

First equation

`\begin{gathered} x=-1 \\ y=-2+3x \\ y=-2+3(-1) \\ y=-2-3 \\ y=-5 \\ \text{ Then, you have the ordered pair} \\ (-1,-5) \end{gathered}`
`\begin{gathered} x=2 \\ y=-2+3x \\ y=-2+3(2) \\ y=-2+6 \\ y=4 \\ \text{ Then, you have the ordered pair} \\ (2,4) \end{gathered}`

Second equation

`\begin{gathered} x=0 \\ y=3-2x \\ y=3-2(0) \\ y=3 \\ \text{ Then you have the ordered pair} \\ (0,3) \end{gathered}`
`\begin{gathered} x=3 \\ y=3-2x \\ y=3-2(3) \\ y=3-6 \\ y=-3 \\ \text{ Then you have the ordered pair} \\ (3,-3) \end{gathered}`

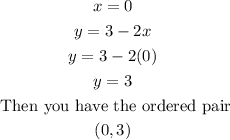
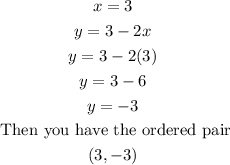
Now, with the points found you can graph the lines that are the limit of the inequalities. So, you have

Finally, it only remains to paint the regions, taking into account the symbols of the inequalities

`\begin{gathered} 3x-y>2 \\ \text{ Subtract 3x from both sides of the equation} \\ 3x-y-3x>2-3x \\ -y>2-3x \\ \text{ Multiply by -1 on both sides of the equation} \\ (-y)\cdot-1>(2-3x)\cdot-1 \\ y<-2+3x \end{gathered}`

`\begin{gathered} 2x+y>3 \\ \text{ Subtract 2x from both sides of the equation} \\ 2x+y-2x>3-2x \\ y>3-2x \end{gathered}`

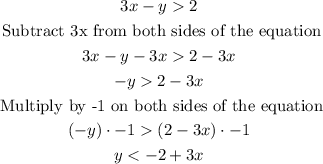
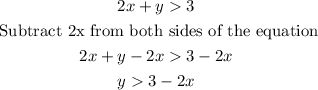
In the case of the first inequality, you can see that y "is less than" the rest of the terms, and in the second inequality, you can see that y "is greater than" the rest of the terms.

Therefore, the graph of the given system of inequalities is