Question

The difference of two supplementary angles is 8 degrees. Find the measures of the angels

Answer 1

86 degrees and 94 degrees

Answer 2

Recall that the supplementary angles sum to 180°

Let x and y are the two angles, so we can write

`x+y=180\degree\quad eq.1`

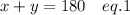
We are given that the difference of the two supplementary angles is 8°

So we can write

`\begin{gathered} x-y=8\degree \\ x=8\degree+y\quad eq.2 \end{gathered}`

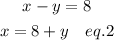
Substitute eq.2 into eq.1

`\begin{gathered} x+y=180\degree \\ (8\degree+y)+y=180\degree \\ 8\degree+2y=180\degree \\ 2y=180\degree-8\degree \\ 2y=172\degree \\ y=(172\degree)/(2) \\ y=86\degree \end{gathered}`

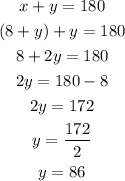
So, one angle is 86°, the other angle is

`\begin{gathered} x=8\degree+y \\ x=8\degree+86\degree \\ x=94\degree \end{gathered}`

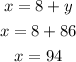
Therefore, the measure of the two angles is

86°, 94°