Question

X^2=49 which numbers are solutions to the equation

Answer 1

So we need to solve the following equation for x:

`x^2=49`

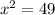
We can apply a square root to both sides but it is important to remember the following property. For any given number a we have:

`\sqrt[]{a^2}=\lvert a\rvert`

Which means that:

`\sqrt[]{a^2}=a\text{ and }\sqrt[]{a^2}=-a`

So for our case we have:

`\begin{gathered} \sqrt[]{x^2}=√(49) \\ \lvert x\rvert=7 \\ x=7\text{ and }x=-7 \end{gathered}`

Then the solutions are 7 and -7.