We know that a line is defined by two points. In this case, we need to find the line equation in the following form:

We need to find the slope, m, and the y-intercept, b. To achieve this, we can use the two-point form of the line:
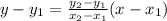
Now, we need to label those two points as follows:
• (3, -4) ---> x1 = 3, y1 = -4.
,
• (-2, -4) ---> x2 = -2, y2 = -4.
And we can substitute those values into the two-point form of the line:
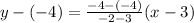
Solving the given operations:
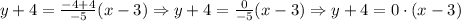
Then
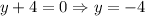
If we need to write the equation in the slope-intercept form, we have that m = 0, and b = -4, then, the equation will be:

In summary, the slope-intercept form of the equation is equal to y = 0x - 4:
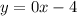
[We can notice that the line is parallel to the x-axis since the slope of the line is equal to 0, m = 0. The y-intercept (the point where the line passes through the y-axis) is equal to b = -4.]
A graph of the line is as follows: