Question

The height of men is a normally distrubuted variable with a mean of 68 inches and a standard deviation of 3 inches.**Round answers to ONE decimal place**a.) What is the minimum height you could be to be considered in the top 10% of tallest men? b.) What is the tallest you could be to be considered in the shortest 15% of men?

Answer 1

For this problem, we are given the mean and standard deviation for the height of men. We need to calculate the minimum height to be considered in the top 10% of tallest men, and the maximum height to be considered in the shortest 15% of men.

The first step we need to solve this problem is to calculate the z-score. The z-score can be found by using the following expression:

`z=(x-\mu)/(\sigma)`

For the first situation, we want a z-score for the top 10% of tallest men. This means that we need to go on the z-table and find the z-score that represents 90% of probability to the left because this will give us the minimum height to be at the 10% tallest. From the z-table we have:

`z=1.29`

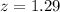
Now we can use the z-score expression to find the value of x. We have:

`\begin{gathered} 1.29=(x-68)/(3) \\ x-68=3.87 \\ x=3.87+68 \\ x=71.87 \end{gathered}`

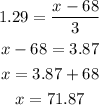
The man should be at least 71.85 inches tall to be considered among the 10% of tallest men.

For the second situation, we have something similar. We need to find the maximum height for a man to be considered between the 15% of men. We need to go into the z-table and find the z-score that produces a result close to 0.15. We have:

`z=-1.04`

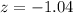
Now we need to use the z-score expression to determine the height:

`\begin{gathered} -1.04=(x-68)/(3) \\ x-68=-3.12 \\ x=68-3.12 \\ x=64.88 \end{gathered}`

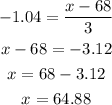
In order to be considered among the smallest men, someone needs to be 64.88 inches tall.