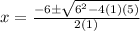Question

X =x² + 6x + 5 = 0b= ] ± √b22-4aaC

Answer 1

We have the following quadratic equation:

`x^2+6x+5=0`

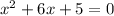
And we have to use the quadratic equation to solve that equation.

1. To find the solutions, we need to start by using the quadratic equation:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ \\ \text{ when }ax^2+bx+c=0 \end{gathered}`

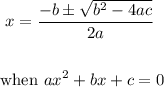
2. Identify a, b, and c from the given quadratic equation:

`\begin{gathered} x^2+6x+5=0 \\ \\ a=1,b=6,c=5 \end{gathered}`

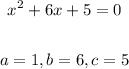
3. Apply the quadratic equation:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ \\ x=(-6\pm√(6^2-4(1)(5)))/(2(1)) \\ \\ \\ \end{gathered}`

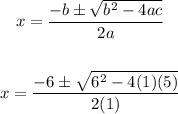
4. And now, we can develop it as follows:

`\begin{gathered} x=(-6\pm√(36-20))/(2) \\ \\ x=(-6\pm√(16))/(2) \\ \\ x=(-6\pm4)/(2) \\ \\ \text{ Therefore:} \\ \\ x=(-6+4)/(2)=-(2)/(2)=-1 \\ \\ x=-1 \\ \\ x=(-6-4)/(2)=(-10)/(2)=-5 \\ \\ x=-5 \end{gathered}`

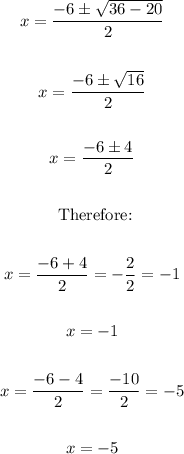
Therefore, we finally have two solutions, x = -1, and x = -5.

Then the first step is given by:

`x=(-6\pm√(6^2-4(1)(5)))/(2(1))`