Question

Find the difference in the volume and total area of a cylinder with both a radius and height of 1.r = 1, h = 1The number of sq units of the total area exceeds the number of cu. units in the volume by

Answer 1

The number of sq units of the total area exceeds the number of cubic units in the volume by 9.43

Step-by-step explanation:

Given that the radius and the height of the cylinder is;

`\begin{gathered} r=1 \\ h=1 \end{gathered}`

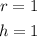
Recall that the formula for the total surface area of a cylinder is;

`A=2\pi r(h+r)`

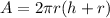
and the volume of a cylinder can be calculated using the formula;

`V=\pi r^2h`

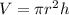
Substituting the given values;

The surface area is;

`\begin{gathered} A=2\pi r(h+r) \\ A=2\pi(1)(1+1) \\ A=2\pi(2) \\ A=4\pi \\ A=12.57\text{ sq units} \end{gathered}`

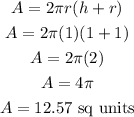
The Volume is;

`\begin{gathered} V=\pi r^2h \\ V=\pi(1)^2(1) \\ V=\pi \\ V=3.14\text{ cubic units} \end{gathered}`

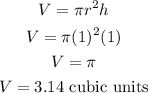
the difference between the volume and the total area of the cylinder is;

`\begin{gathered} difference=A-V \\ d=12.57-3.14 \\ =9.43 \end{gathered}`

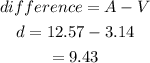
Therefore, the number of sq units of the total area exceeds the number of cubic units in the volume by 9.43