Given the system of equations:
-4x + y = 5
-2y = -8x + 4
To solve the system of equations by graphing, apply the slope-intercept form:
y = mx + b
Where m is the slope and b is the y-intercept.
Rewrite each equation to slope-intercept form
Equation 1:
-4x + y = 5
Add 4x to both sides:
-4x + 4x + y = 4x + 5
y = 4x + 5
Equation 2:
-2y = -8x + 4
Divide all terms by -2:
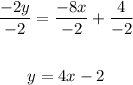
We have the equations in slope intercept form:
y = 4x + 5
y = 4x - 2
From the slope intercept form of both equatios, we can see both equations have the same slope.
Slope = 4
Since they have the same slope, they are parallel lines.
The solution will be the points of intersections, but parallel lines do not intersect.
Therefore, we can say the system has no solution.
We have the graph below:
From the graph above, both lines do not intersect. Therefore, there is no solution.
ANSWER:
No solution