From the problem :

Factor completely :
We need to find the factors of 10 and 7
We have :
10 = 1 x 10
10 = 2 x 5
7 = 1 x 7
We will do trial and error, The sum of the product of the factors must be equal to the middle term which is 19
Let's say for 10 = 1 x 10 and 7 = 1 x 7
(1 x 7) + (1 x 10) = 17 not equal to 19
(7 x 10) + (1 x 1) = 71 not equal to 19
try the other factors of 10.
10 = 2 x 5 and 7 = 1 x 7
(2 x 7) + (5 x 1) = 19 Equal to 19
Now we have the factors, let's arrange in this way :
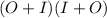
O will be the outer and I will be the inner.
O is the paired factors of 10 and 7
For O, we have 2 and 7
For I, we have 5 and 1
This will be :
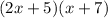
The answer is (2x + 5)(x + 7)