The function
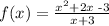
let f(x) = y
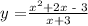
substitute x = 0
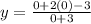

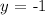
(x = 0 and y = -1)
Next, put y = 0 in the function and then solve for x
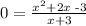
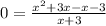
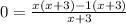
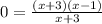

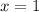
(x = 1 and y =0)
The domain is (0 and 1)
The x -intercept is (1, 0)
The hole is
x + 3 =0
x= -3 is the hole
To find the horizontal asymptote;
since the degree of the numerator is greater than the denominator, then it has no horiizontal asymptote
horizontal asymptote = none