Given the expressions:
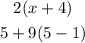
You need to remember that the Distributive Property states that:
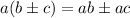
• In order to simplify the first expression, you only need to apply the Distributive Property, because there is a number multiplying a Sum. Therefore, get:
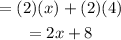
• In order to simplify the second expression, you need to follow these steps:
1. Apply the Distributive Property:
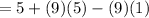

2. Solve the Addition:
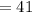
Hence, the answers are:
• The first problem requires to use only the Distributive Property to simplify it. It is required because there is a number multiplying a Sum:

Notice that the second expression can be simplified using the Distributive Property as the first step.
• The second problem can be simplified by applying the Distributive Property and then adding the numbers.