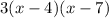To solve a question like this, you will need to factorise the first term of the expression out.
So, our expression becomes
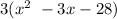
Now, you will need to find the factors of 28 whose sum will give you -3
Always remember to express it in terms of x.
The answer to that is -7x and +4x. Thus we can rewrite the expression as;
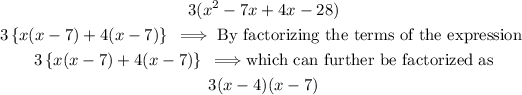
In summary 3x^2-9x-84 can be factorized as