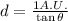Question

Need help with this review question. More explanation and how far is the star from the sun in astronomical units? Also how do I write an expression to calculate d for any of the stars

Answer 1

To solve this problem, we will use the trigonometric function tangent. Recall that by definition in a right triangle:

`\tan \theta=\frac{opposite\text{ leg}}{\text{adjacent leg}}\text{.}`

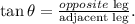
In the given diagram, opposite leg=1 A.U. ( astronomical unit), θ=0.00001389°, and adjacent leg =d, therefore:

`\tan (0.00001389)=(1)/(d)\text{.}`

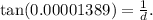
Solving the above equation for d, we get:

`d=\frac{1A.U\text{.}}{\text{tan(}0.00001389)}\text{.}`

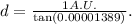
Simplifying, we get:

`d=4124966.128\text{ A.U.}`

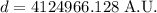
Answer:

`d=4124966.128\text{ A.U.}`

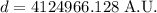
For any star, if we are given an angle θ, we can use the following expression to determine its distance from the Sun:

`d=\frac{1A.U\text{.}}{\tan\theta}`