For the smaller sphere with mass M and radius, R the moment of inertia is
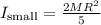
For the larger sphere with mass M and radius 2R the moment of Intertia is
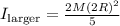
The ratio between the larger and the small spheres can be calculated as
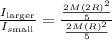
we simplify
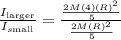

ANSWER
The ratio is 4
b. 4