Question

Given the sum of the reciprocal of two numbers is 1/6 and the product of these two numbers is -48. What are those two numbers

Answer 1

Given:

the sum of the reciprocals of two numbers is 1/6

Let the numbers are (x) and (y)

so,

`(1)/(x)+(1)/(y)=(1)/(6)\rightarrow(1)`

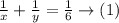
And, the product of these two numbers is -48

so,

`x\cdot y=-48\rightarrow(2)`

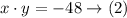
from equation (2):

`\begin{gathered} y=-(48)/(x) \\ \\ (1)/(y)=-(x)/(48)\rightarrow(3) \end{gathered}`

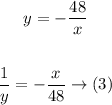
substitute with (1/y) from equation (3) into equation (1) then solve for (x):

`\begin{gathered} (1)/(x)-(x)/(48)=(1)/(6) \\ (48-x^2)/(48x)=(1)/(6) \end{gathered}`

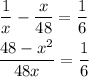
Using the cross product:

`\begin{gathered} 48x=6(48-x^2)\rightarrow(/6) \\ 8x=48-x^2 \\ x^2+8x-48=0 \\ (x-4)(x+12)=0 \\ x-4=0\rightarrow x=4 \\ x+12=0\rightarrow x=-12 \end{gathered}`

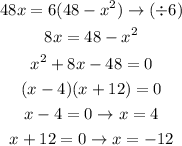
We will substitute the value of (x) into equation (2) to find (y)

`\begin{gathered} x=4\rightarrow y=-(48)/(4)=-12 \\ \\ x=-12\rightarrow y=-(48)/(-12)=4 \end{gathered}`

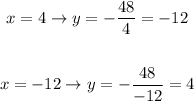
so, the answer will be the numbers are: -12 and 4