Question

Solve for y and x: X = y -8 and -X - y = 0

Answer 1

We must solve the following system of equation:

`\begin{gathered} x=y-8 \\ -x-y=0 \end{gathered}`

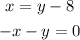
Solving by elimination method.

If we add the first equation wih the second one, we obtain

`x-x-y=y-8+0`

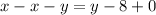
which is equal to

`-y=y-8`

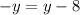
If we move y to the left hand side, we have

`\begin{gathered} -y-y=-8 \\ \\ \end{gathered}`

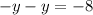
and it reads

`\begin{gathered} -2y=-8 \\ y=(-8)/(-2) \\ y=4 \end{gathered}`

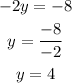
We obtained the first result y=4. Now, we can substitute this value into one of the two equation. If we substitute y=4 in the first equation, we have

`x=4-8`

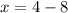
which gives x=-4. Finally, the answer is x=-4 and y=4. The coordinate of this solution is (-4,4).