First, we need to figure the reaction out.
Both reactants are ionic compounds, so their reaction is probably a double displacemente reaction.
The Cl has a charge of 1-, so Fe has a charge of 2+. Na has a charge of +1 and PO₄ has a charge of 3-.
To combine Fe²⁺ with PO₄³⁻, we will need 3 Fe²⁺ and 2 PO₄³⁻, so the compound becomes neutral.
Both Na and Cl have single charge, so their combination is simply 1 Na and 1 Cl.
So, the products are Fe₃(PO₄)₂ and NaCl, so the unbalanced reaction is:
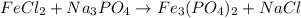
To balance it, We can start by putting a coefficient of 2 on Na₃PO₄, so we have two PO₄³⁻ anions on both sides:
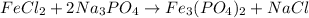
Now, we put a coefficient of 3 on FeCl₂ and 6 on NaCl to get the balanced equation:
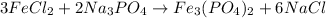
Now, we first need to calculate the number of moles of each reactant, using their molar masses:
![\begin{gathered} M_(FeCl_2)=1\cdot M_(Fe)+2\cdot M_(Cl)=(1\cdot55.845+2\cdot35.453)g/mol=126.751g/mol \\ M_(Na_3PO_4)=3\cdot M_(Na)+1\cdot M_P+4\cdot M_O=(3\cdot22.98976928+1\cdot30.973762+4\cdot15.9994)g/mol=163.94066984g/mol \end{gathered}]()
So:
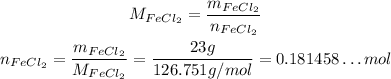
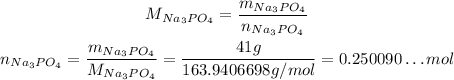
Now, if the coefficient of FeCl₂ is 3, for each 3 FeCl₂ that reacts, one reaction occurs, so the number of reactions that will need to occur to consume all its number of moles is that amount over 3:
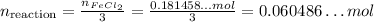
Similarly, we get the number of reactions that would occur if all Na₃PO₄ reacts by dividing its number of moles by its coefficient, that is 2:
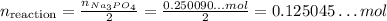
This means that the amount we have of FeCl₂ is enough for only about 0.0605 mol of reactions while the amount we have of Na₃PO₄ is enought for about 0.1250 mol of reactions, which is more than the other reactant.
This means that the reactant that limits the amount of reaction that can occur is FeCl₂, so the limiting reactant is FeCl₂.