we know that
Focus (0,-1)
Directrix is the line y=0
so
we have a vertical parabola open downward
Remember that
The distance from the vertex to the directrix must be the same that the distance from the vertex to the focus
which means
The vertex is the point (0,-0.5) ----> midpoint between the focus and the directrix
Find out the value of p (focal distance)
p=0.5
The equation of the parabola is given by
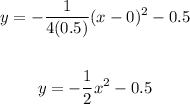
The vertex is (0,-0.5)
The value of p=0.5