Question

What are the solutions to the quadratic equation below? x² -2x -168=0

Answer 1

-12 and 14.

Step-by-step explanation:

Given the quadratic equation: x² -2x -168=0​

First, we factorize the expression on the left-hand side.

`x^2-2x-168=(x\text{ )(x )}`

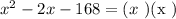
Next, we multiply the first and last term,

`-168* x^2=-168x^2`

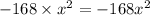
We then write factors of -168.

`\begin{gathered} -168=12\text{ and -14 } \\ -168=-12\text{ and 14} \\ \text{Add the factors:} \\ \text{12-14=-2} \\ -12+14=2 \end{gathered}`

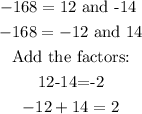
We pick the factors that add up to the middle term: -2

`\begin{gathered} x^2-2x-168=0 \\ (x+12)(x-14)=0 \\ x+12=0\text{ or }x-14=0 \\ x=-12\text{ or x=14} \end{gathered}`

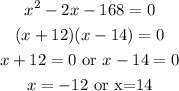
The solutions to the quadratic equation are -12 and 14.